Open CASCADE Technology: Modeling Data
Introduction Modeling Data supplies data structures to represent 2D and 3D geometric models. This manual explains how to use Modeling Data. Geometry Utilities Geometry Utilities provide the following services: Creation of shapes by interpolation and approx
dev.opencascade.org
Bounding boxes
Bounding boxe는 많은 OCCT 알고리즘에서 사용됨.
가령 shape 쌍의 간섭 체크량이 과도하지 않도록 해주는 필터 (bounding box간 간섭체크가 실 간섭체크보다 훨씬 간단).
bounding box의 2가지 타입:
- axis-aligned bounding box (AABB) : box의 edge들이 World Coordinate System (WCS)의 축들에 평행.
- oriented BndBox (OBB) : 자신의 좌표계. 사실, AABB 는OBB의 특수한 case임.
아래 그림은 OBB가 AABB보다 나는 경우:
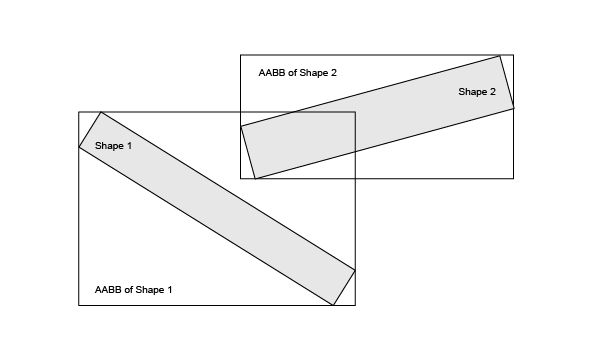
위 그림에서 AABB는 서로 간섭하므로, OCCT 알고리즘은 shape 간섭 계산에 더 많은 시간을 씀.OBB를 검사한다면 간섭하지 않으므로, shape 간섭 계산을 필요하지 않다.OBB 생성과 분석이 AABB보다 훨씬 많은 시간이 소요된다.
최소 surface를 가지는 bounding box를 optimal이라 부른다.
OCCT에서 bounding box는 Bnd package에 정의된다. Bnd_Box가 AABB를 정의하고, Bnd_OBB가 OBB를 정의한다. 이 클래스들은 다음 메소드를 포함한다.
- IsVoid method indicates whether the bounding box is empty (uninitialized).
- SetVoid method clears the existing bounding box.
- Enlarge(...) extends the current bounding box.
- Add(...) extends the bounding box as necessary to include the object (a point, a shape, etc.) passed as the argument.
- IsOut(...) checks whether the argument is inside/outside of the current BndBox.
BRepBndLib 클래스가 shape로부터의 bounding box (AABB, OBB 모두)의 생성 메소드를 포함.
Brief description of some algorithms working with OBB
Creation of OBB from set of points
이 알고리즘은 "Fast Computation of Tight Fitting Oriented Bounding Boxes" by Thomas Larsson and Linus Källberg (FastOBBs.pdf) 에 설명되어 있다.
절차:
Open CASCADE Technology: Modeling Data
Introduction Modeling Data supplies data structures to represent 2D and 3D geometric models. This manual explains how to use Modeling Data. Geometry Utilities Geometry Utilities provide the following services: Creation of shapes by interpolation and approx
dev.opencascade.org
Creation of Optimal OBB from set of points
point 집합에서의 optimal OBB 생성을 위해서는 위 설명과 같은 알고리즘이 사용되지만, 로직은 좀 더 단순하게 하며, 계산 시간은 더 길다.
극점들에 의해 생성된 모든 가능한 축을 체크해야 한다.
그리고 극점들은 초기 축에만 유효하기 때문에, 각 축에 점의 전체 집합을 투영해야 한다. 이 접근법은 일반적으로 훨씬 더 엄격한 OBB를 제공하지만 성능은 더 낮다. 알고리즘의 복잡성은 여전히 선형이며 점 집합에 BVH(Bounding Volume Hierarchy)를 사용하면 O(N + C*log(N))이다.
125K node 집합을 사용하는 모델에 대한 optimal OBB, not optimal OBB 예:
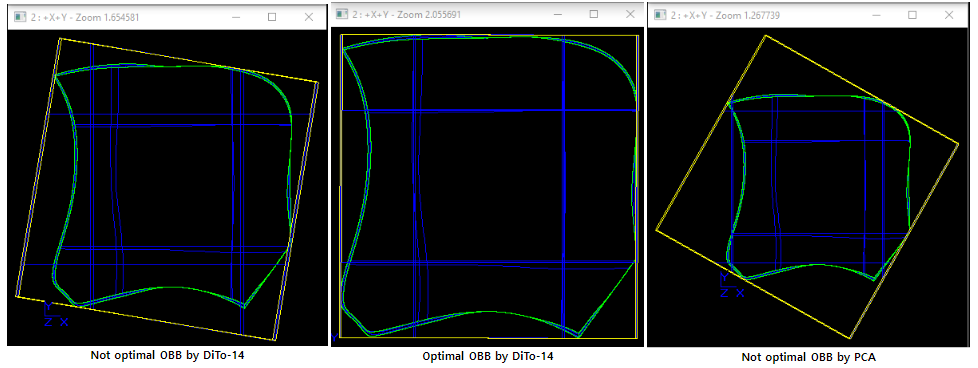
계산시간:
not optimal OBB : 0.007sec
optimal : 0.1sec (14배)
PCA (Principal Component Analysis)접근 방법 : 0.17sec
PCA알고리즘인 BRepBndLib::AddOBB 메소드에서 IsOptimal 플래그로 조정됨.
알고리즘들은 Bnd_OBB::ReBuild(...) 메소드에 구현되어 있다.
Creation of OBB based on Axes of inertia
절차:
- Calculate three inertia axes, which will be the axes of the OBB.
- Transform the source object *(TopoDS_Shape)* into the local coordinate system based on the axes from item 1.
- Create an AABB for the shape obtained in the item 2.
- Compute the center of AABB and its half dimensions.
- Transform the center into the WCS.
- Create OBB using the center, axes and half dimensions.
Method IsOut for a point
- Project the point to each axis.
- Check, whether the absolute value of the projection parameter greater than the correspond half-dimension. In this case, IsOut method will return TRUE.
Method IsOut for another OBB
"Separating Axis Theorem for Oriented Bounding Boxes" 에 의하면, 15개의 separating axes를 체크해야 한다:
box들의 6개 축, cross product들의 9개 축.

적어도 한 축(15개 중)에서 간섭이 없을 경우, OBB는 전혀 간섭이 없다.
Method Add for point or another bounding box
source point와 주어진 bounding box들의 모든 vertex들을 기반으로 새로운 OBB를 생성한다. (Creation of OBB from set of points)
Add a shape
BRepBndLib::AddOBB(...) 메소드는 complex object (TopoDS_Shape)에서 bounding box를 생성한다.
이 메소드는 Creation of OBB from set of points 와 Creation of OBB based on Axes of inertia 에서 설명된 알고리즘을 모두 사용한다.
shape의 바깥 shell이 담고 있는 point 집합으로 표현될 수 있으면 첫 알고리즘이 사용된다.
- Nodes of triangulation;
- Nodes of Poly_Polygon3D;
- Vertices of edges with a linear 3D-curve lying in the planar face;
- Vertices of edges with a linear 3D-curve if the source shape does not contain a more complex topological structure (e.g. the source shape is a compound of edges);
- Vertices if the source shape does not contain a more complex topological structure (e.g. the source shape is a compound of vertices).
point들이 추출될 수 없으면, Creation of OBB based on Axes of inertia 의 알고리즘이 사용된다.
package BRepBndLib는 shape의 AABB 생성을 위해 BRepBndLib::Add(...), BRepBndLib::AddClose(...), BRepBndLib::AddOptimal(...) 메소드를 포함하고 있다. 참조메뉴얼을 참고할 것.
Limitations of algorithm for OBB creation
1. Creation of OBB from set of points 절에서 설명된 알고리즘이 Creation of OBB based on Axes of inertia 알고리즘 보다 훨씬 잘 동작하고 (더 적은 surface의 OBB 생성), 더 빠르다. 그럼에도 불구하고, (일반적으로) 두 알고리즘의 결과는 항상 optimal은 아니다. 더우기, 첫 메소드는 복잡한 geometry의 shape의 OBB 계산은 불가하다.
2. 현재는 OBB 알고리즘 생성은 3D 공간의 object에 대해서만 구현되어 있다.

